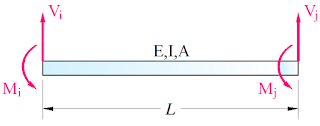
Análisis de la matriz de rigidez por filas

Análisis de la matriz de rigidez por filas

  17:54    ZEOMATH

---

Considere un elemento prismático de eje recto y sección constante, sometido a fuerzas y momentos concentrados en sus extremos.

La matriz de rigidez «K» describe el comportamiento del elemento con referencia a ciertos grados de libertad, a cada uno de los cuales se asigna una componente de desplazamiento y una componente de fuerza. Se dice así que el elemento tiene seis grados de libertad.

$$K=\begin{bmatrix} \frac { EA }{ L }  & 0 & 0 & -\frac { EA }{ L }  & 0 & 0 \\ 0 & \frac { 12EI }{ { L }^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  & 0 & -\frac { 12EI }{ { L }^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  \\ -\frac { EA }{ L }  & 0 & 0 & \frac { EA }{ L }  & 0 & 0 \\ 0 & -\frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  & 0 & \frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  \end{bmatrix}$$

FILA 1 DE LA MATRIZ DE RIGIDEZ.

$${ u }_{ 1 }=\frac { { H }_{ 1 }L }{ EA } \\ { H }_{ 1 }=\frac { EA }{ L } { u }_{ 1 }\\ { H }_{ 4 }=-\frac { EA }{ L } { u }_{ 1 }$$

Los valores ubicados en la fila 1 de la matriz de rigidez, se deducen asignando un desplazamiento unitario en el grado de libertad 1, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ u }_{ 1 }=1\\ { H }_{ 1 }=\frac { EA }{ L } \\ { H }_{ 4 }=-\frac { EA }{ L } $$

$${ k }_{ 11 }=\frac { EA }{ L } \\ { k }_{ 14 }=-\frac { EA }{ L }$$

k11 y k14 son las fuerzas necesarias en los grados de libertad 1 y 4 respectivamente, para producir un desplazamiento unitario en el grado de libertad 1, restringiendo todo movimiento (traslación o giro) en los demás grados de libertad.

FILA 2 DE LA MATRIZ DE RIGIDEZ.

$${ V }_{ 2 }=12\frac { EI }{ { L }^{ 3 } } { u }_{ 2 }\\ { M }_{ 3 }=6\frac { EI }{ { L }^{ 2 } } { u }_{ 2 }\\ { V }_{ 5 }=-{ V }_{ 2 }=-12\frac { EI }{ { L }^{ 3 } } { u }_{ 2 }\\ { M }_{ 6 }=6\frac { EI }{ { L }^{ 2 } } { u }_{ 2 }$$

Los valores ubicados en la fila 2 de la matriz de rigidez, se deducen asignando un desplazamiento unitario en el grado de libertad 2, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ u }_{ 2 }=1\\ { V }_{ 2 }=12\frac { EI }{ { L }^{ 3 } } \\ { M }_{ 3 }=6\frac { EI }{ { L }^{ 2 } } \\ { V }_{ 5 }=-{ V }_{ 2 }=-12\frac { EI }{ { L }^{ 3 } } \\ { M }_{ 6 }=6\frac { EI }{ { L }^{ 2 } } $$

$${ k }_{ 22 }=\frac { 12EI }{ { L }^{ 3 } } \\ { k }_{ 23 }=\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 25 }=-\frac { 12EI }{ { L }^{ 3 } } \\ { k }_{ 26 }=\frac { 6EI }{ { L }^{ 2 } } $$

k22, k23, k25, k26 son las fuerzas (y momentos) necesarios en los grados de libertad 2, 3, 5, 6 para producir un desplazamiento unitario en el grado de libertad 2, restringiendo todo movimiento (traslación o giro) en los demás grados de libertad.

FILA 3 DE LA MATRIZ DE RIGIDEZ.

$${ V }_{ 2 }=6\frac { EI }{ { L }^{ 2 } } { \theta  }_{ 3 }\\ { M }_{ 3 }=4\frac { EI }{ L } { \theta  }_{ 3 }\\ { V }_{ 5 }=-{ V }_{ 2 }=-6\frac { EI }{ { L }^{ 2 } } { \theta  }_{ 3 }\\ { M }_{ 6 }=2\frac { EI }{ L } { \theta  }_{ 3 }$$

Los valores ubicados en la fila 3 de la matriz de rigidez, se deducen asignando un giro unitario en el grado de libertad 3, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ \theta  }_{ 3 }=1\\ { V }_{ 2 }=6\frac { EI }{ { L }^{ 2 } } \\ { M }_{ 3 }=4\frac { EI }{ L } \\ { V }_{ 5 }=-{ V }_{ 2 }=-6\frac { EI }{ { L }^{ 2 } } \\ { M }_{ 6 }=2\frac { EI }{ L } $$

$${ k }_{ 32 }=\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 33 }=\frac { 4EI }{ L } \\ { k }_{ 35 }=-\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 36 }=\frac { 2EI }{ L } $$

k32, k33, k35, k36 son las fuerzas (y momentos) necesarios en los grados de libertad 2, 3, 5, 6 para producir un desplazamiento unitario en el grado de libertad 3, restringiendo todo movimiento (traslación o giro) en los demás grados de libertad.

FILA 4 DE LA MATRIZ DE RIGIDEZ.

$${ u }_{ 4 }=\frac { { H }_{ 4 }L }{ EA } \\ { H }_{ 4 }=\frac { EA }{ L } { u }_{ 4 }\\ { H }_{ 1 }=-\frac { EA }{ L } { u }_{ 4 }$$

Los valores ubicados en la fila 4 de la matriz de rigidez, se deducen asignando un desplazamiento unitario en el grado de libertad 4, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ u }_{ 4 }=1\\ { H }_{ 1 }=-\frac { EA }{ L } \\ { H }_{ 4 }=\frac { EA }{ L } $$

$${ k }_{ 41 }=-\frac { EA }{ L } \\ { k }_{ 44 }=\frac { EA }{ L } $$

k41, k44 son las fuerzas necesarias en los grados de libertad 1, 4 para producir un desplazamiento unitario en el grado de libertad 4, restringiendo todo movimiento (traslación o giro) en todos los demás grados de libertad.

FILA 5 DE LA MATRIZ DE RIGIDEZ.

$${ V }_{ 2 }=-12\frac { EI }{ { L }^{ 3 } } { u }_{ 5 }\\ { M }_{ 3 }=-6\frac { EI }{ { L }^{ 2 } } { u }_{ 5 }\\ { V }_{ 5 }=-{ V }_{ 2 }=12\frac { EI }{ { L }^{ 3 } } { u }_{ 5 }\\ { M }_{ 6 }=-6\frac { EI }{ { L }^{ 2 } } { u }_{ 5 }$$

Los valores ubicados en la fila 5 de la matriz de rigidez, se deducen asignando un desplazamiento unitario en el grado de libertad 5, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ u }_{ 5 }=1\\ { V }_{ 2 }=-12\frac { EI }{ { L }^{ 3 } } \\ { M }_{ 3 }=-6\frac { EI }{ { L }^{ 2 } } \\ { V }_{ 5 }=-{ V }_{ 2 }=12\frac { EI }{ { L }^{ 3 } } \\ { M }_{ 6 }=-6\frac { EI }{ { L }^{ 2 } } $$

$${ k }_{ 52 }=-\frac { 12EI }{ { L }^{ 3 } } \\ { k }_{ 53 }=-\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 55 }=\frac { 12EI }{ { L }^{ 3 } } \\ { k }_{ 56 }=-\frac { 6EI }{ { L }^{ 2 } } $$

k52, k53, k55, k56 son las fuerzas (y momentos) necesarios en los grados de libertad 2, 3, 5, 6 para producir un desplazamiento unitario en el grado de libertad 5, restringiendo todo movimiento (traslación o giro) en los demás grados de libertad.

FILA 6 DE LA MATRIZ DE RIGIDEZ.

$${ V }_{ 2 }=6\frac { EI }{ { L }^{ 2 } } { \theta  }_{ 6 }\\ { M }_{ 3 }=2\frac { EI }{ L } { \theta  }_{ 6 }\\ { V }_{ 5 }=-{ V }_{ 2 }=-6\frac { EI }{ { L }^{ 2 } } { \theta  }_{ 6 }\\ { M }_{ 6 }=4\frac { EI }{ L } { \theta  }_{ 6 }$$

Los valores ubicados en la fila 6 de la matriz de rigidez, se deducen asignando un giro unitario en el grado de libertad 6, al mismo tiempo que se restringe todo movimiento (traslación o giro) en las demás componentes de desplazamiento.

$${ \theta  }_{ 6 }=1\\ { V }_{ 2 }=6\frac { EI }{ { L }^{ 2 } } \\ { M }_{ 3 }=2\frac { EI }{ L } \\ { V }_{ 5 }=-{ V }_{ 2 }=-6\frac { EI }{ { L }^{ 2 } } \\ { M }_{ 6 }=4\frac { EI }{ L } $$

$${ k }_{ 62 }=\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 63 }=\frac { 2EI }{ L } \\ { k }_{ 65 }=-\frac { 6EI }{ { L }^{ 2 } } \\ { k }_{ 66 }=\frac { 4EI }{ L } $$

k62, k63, k65, k66 son las fuerzas (y momentos) necesarios en los grados de libertad 2, 3, 5, 6 para producir un desplazamiento unitario en el grado de libertad 6, restringiendo todo movimiento (traslación o giro) en los demás grados de libertad.

ANÁLISIS DE LA MATRIZ DE RIGIDEZ POR COLUMNAS.

Debido a que la matriz de rigidez es simétrica, el mismo análisis puede realizarse por columnas.

Los valores de la columna 1 de la matriz de rigidez, son las fuerzas necesarias en cada grado de libertad para producir un desplazamiento unitario en el grado de libertad 1, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Los valores de la columna 2 de la matriz de rigidez, son las fuerzas y momentos necesarios en cada grado de libertad para producir un desplazamiento unitario en el grado de libertad 2, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Los valores de la columna 3 de la matriz de rigidez, son las fuerzas y momentos necesarios en cada grado de libertad para producir un giro unitario en el grado de libertad 3, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Los valores de la columna 4 de la matriz de rigidez, son las fuerzas necesarias en cada grado de libertad para producir un desplazamiento unitario en el grado de libertad 4, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Los valores de la columna 5 de la matriz de rigidez, son las fuerzas y momentos necesarios en cada grado de libertad para producir un desplazamiento unitario en el grado de libertad 5, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Los valores de la columna 6 de la matriz de rigidez, son las fuerzas y momentos necesarios en cada grado de libertad para producir un giro unitario en el grado de libertad 6, al mismo tiempo que se restringe todo movimiento (traslación o giro) en los demás grados de libertad.

Read More

Matriz de rigidez de un elemento estructural

Matriz de rigidez de un elemento estructural

  11:06    ZEOMATH

---

Considere un elemento prismático de eje recto y sección constante, sometido a fuerzas y momentos concentrados en sus extremos.

Las relaciones entre las fuerzas y los desplazamientos de los nudos, se hallarán asignando un valor arbitrario a una componente de desplazamiento, mientras todas las demás componentes de desplazamiento permanecen iguales a cero.

CARGA AXIAL.

Si se impide todo movimiento en el extremo j, existirán las siguientes relaciones entre las fuerzas y los desplazamientos:

$$u_{ i }=\frac { H_{ i }^{ I }L }{ EA } \\ H_{ i }^{ I }=\frac { EA }{ L } u_{ i }$$

$$H_{ j }^{ I }=-H_{ i }^{ I }\\ H_{ j }^{ I }=-\frac { EA }{ L } u_{ i }$$

Si se impide todo movimiento en el extremo i, existirán las siguientes relaciones entre las fuerzas y los desplazamientos:

$$u_{ j }=\frac { H_{ j }^{ II }L }{ EA } \\ H_{ j }^{ II }=\frac { EA }{ L } u_{ j }$$

$$H_{ i }^{ II }=-H_{ j }^{ II }\\ H_{ i }^{ II }=-\frac { EA }{ L } u_{ j }$$

Finalmente:

$$H_{ i }=H_{ i }^{ I }+H_{ i }^{ II }\\ H_{ i }=\frac { EA }{ L } u_{ i }-\frac { EA }{ L } u_{ j }$$

$$H_{ j }=H_{ j }^{ I }+H_{ j }^{ II }\\ H_{ j }=-\frac { EA }{ L } u_{ i }+\frac { EA }{ L } u_{ j }$$

FUERZA CORTANTE Y MOMENTO FLECTOR.

Para deducir la relación entre las fuerzas y los desplazamientos, usaremos las ecuaciones de pendiente y deflexión.

$$M_{ i }=\frac { 2EI }{ L } (2θ_{ i }+θ_{ j }-3ψ)\\ ψ=\frac { v_{ j }-v_{ i } }{ L } $$

$$M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ L } ψ\\ M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ L } \left( \frac { v_{ j }-v_{ i } }{ L }  \right) \\ M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }\\ M_{ i }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 4EI }{ { L } } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }$$

$$M_{ j }=\frac { 2EI }{ L } (θ_{ i }+2θ_{ j }-3ψ)\\ ψ=\frac { v_{ j }-v_{ i } }{ L } $$

$$M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ L } ψ\\ M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ L } \left( \frac { v_{ j }-v_{ i } }{ L }  \right) \\ M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }\\ M_{ j }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 4EI }{ L } θ_{ j }$$

$$V_{ i }=\frac { M_{ i }+M_{ j } }{ L } \\ M_{ i }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 4EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }\\ M_{ j }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } v_{ j }+\frac { 4EI }{ L } θ_{ j }\\ M_{ i }+M_{ j }=\frac { 12EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 6EI }{ L } θ_{ i }-\frac { 12EI }{ { L }^{ 2 } } v_{ j }+\frac { 6EI }{ L } θ_{ j }\\ \frac { M_{ i }+M_{ j } }{ L } =\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ { L }^{ 2 } } θ_{ i }-\frac { 12EI }{ { L }^{ 3 } } v_{ j }+\frac { 6EI }{ { L }^{ 2 } } θ_{ j }\\ { V }_{ i }=\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ { L }^{ 2 } } θ_{ i }-\frac { 12EI }{ { L }^{ 3 } } v_{ j }+\frac { 6EI }{ { L }^{ 2 } } θ_{ j }$$

$$V_{ j }=-V_{ i }\\ V_{ j }=-\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }-\frac { 6EI }{ { L }^{ 2 } } θ_{ i }+\frac { 12EI }{ { L }^{ 3 } } { v }_{ j }-\frac { 6EI }{ { L }^{ 2 } } θ_{ j }$$

NOTACIÓN MATRICIAL.

$$H_{ i }=\frac { EA }{ L } u_{ i }-\frac { EA }{ L } u_{ j }\\ V_{ i }=\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ L^{ 2 } } θ_{ i }-\frac { 12EI }{ L^{ 3 } } v_{ j }+\frac { 6EI }{ L^{ 2 } } θ_{ j }\\ M_{ i }=\frac { 6EI }{ L^{ 2 } } { v }_{ i }+\frac { 4EI }{ L } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }\\ H_{ j }=-\frac { EA }{ L } u_{ i }+\frac { EA }{ L } u_{ j }\\ V_{ j }=-\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }-\frac { 6EI }{ L^{ 2 } } θ_{ i }+\frac { 12EI }{ L^{ 3 } } v_{ j }-\frac { 6EI }{ L^{ 2 } } θ_{ j }\\ M_{ j }=\frac { 6EI }{ L^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 4EI }{ L } θ_{ j }$$

Las relaciones fuerza desplazamiento pueden expresarse en notación matricial, así:

$$\begin{bmatrix} \frac { EA }{ L }  & 0 & 0 & -\frac { EA }{ L }  & 0 & 0 \\ 0 & \frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  & 0 & -\frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ L^{ 2 } }  & \frac { 4EI }{ L }  & 0 & -\frac { 6EI }{ L^{ 2 } }  & \frac { 2EI }{ L }  \\ -\frac { EA }{ L }  & 0 & 0 & \frac { EA }{ L }  & 0 & 0 \\ 0 & -\frac { 12EI }{ L^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  & 0 & \frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  \end{bmatrix}\begin{Bmatrix} { u }_{ i } \\ { \upsilon  }_{ i } \\ { \theta  }_{ i } \\ { u }_{ j } \\ { \upsilon  }_{ j } \\ { \theta  }_{ j } \end{Bmatrix}=\begin{Bmatrix} { H }_{ i } \\ { V }_{ i } \\ { M }_{ i } \\ { H }_{ j } \\ { V }_{ j } \\ { M }_{ j } \end{Bmatrix}$$

Donde:

$$K=\begin{bmatrix} \frac { EA }{ L }  & 0 & 0 & -\frac { EA }{ L }  & 0 & 0 \\ 0 & \frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  & 0 & -\frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ L^{ 2 } }  & \frac { 4EI }{ L }  & 0 & -\frac { 6EI }{ L^{ 2 } }  & \frac { 2EI }{ L }  \\ -\frac { EA }{ L }  & 0 & 0 & \frac { EA }{ L }  & 0 & 0 \\ 0 & -\frac { 12EI }{ L^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  & 0 & \frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  \end{bmatrix}$$

«K» es la matriz de rigidez del elemento.

$$u=\begin{Bmatrix} { u }_{ i } \\ { \upsilon  }_{ i } \\ { \theta  }_{ i } \\ { u }_{ j } \\ { \upsilon  }_{ j } \\ { \theta  }_{ j } \end{Bmatrix}$$

«u» es el vector de desplazamiento (traslaciones y giros).

$$f=\begin{Bmatrix} { H }_{ i } \\ { V }_{ i } \\ { M }_{ i } \\ { H }_{ j } \\ { V }_{ j } \\ { M }_{ j } \end{Bmatrix}$$

«f» es el vector de fuerzas (y momentos).

Read More