Matriz de rigidez de un elemento estructural

Matriz de rigidez de un elemento estructural

  11:06    ZEOMATH

---

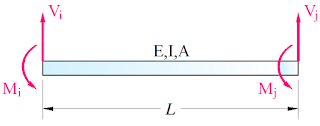
Considere un elemento prismático de eje recto y sección constante, sometido a fuerzas y momentos concentrados en sus extremos.

Las relaciones entre las fuerzas y los desplazamientos de los nudos, se hallarán asignando un valor arbitrario a una componente de desplazamiento, mientras todas las demás componentes de desplazamiento permanecen iguales a cero.

CARGA AXIAL.

Si se impide todo movimiento en el extremo j, existirán las siguientes relaciones entre las fuerzas y los desplazamientos:

$$u_{ i }=\frac { H_{ i }^{ I }L }{ EA } \\ H_{ i }^{ I }=\frac { EA }{ L } u_{ i }$$

$$H_{ j }^{ I }=-H_{ i }^{ I }\\ H_{ j }^{ I }=-\frac { EA }{ L } u_{ i }$$

Si se impide todo movimiento en el extremo i, existirán las siguientes relaciones entre las fuerzas y los desplazamientos:

$$u_{ j }=\frac { H_{ j }^{ II }L }{ EA } \\ H_{ j }^{ II }=\frac { EA }{ L } u_{ j }$$

$$H_{ i }^{ II }=-H_{ j }^{ II }\\ H_{ i }^{ II }=-\frac { EA }{ L } u_{ j }$$

Finalmente:

$$H_{ i }=H_{ i }^{ I }+H_{ i }^{ II }\\ H_{ i }=\frac { EA }{ L } u_{ i }-\frac { EA }{ L } u_{ j }$$

$$H_{ j }=H_{ j }^{ I }+H_{ j }^{ II }\\ H_{ j }=-\frac { EA }{ L } u_{ i }+\frac { EA }{ L } u_{ j }$$

FUERZA CORTANTE Y MOMENTO FLECTOR.

Para deducir la relación entre las fuerzas y los desplazamientos, usaremos las ecuaciones de pendiente y deflexión.

$$M_{ i }=\frac { 2EI }{ L } (2θ_{ i }+θ_{ j }-3ψ)\\ ψ=\frac { v_{ j }-v_{ i } }{ L }$$

$$M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ L } ψ\\ M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ L } \left( \frac { v_{ j }-v_{ i } }{ L }  \right) \\ M_{ i }=\frac { 4EI }{ L } θ_{ i }+\frac { 2EI }{ L } θ_{ j }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }\\ M_{ i }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 4EI }{ { L } } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }$$

$$M_{ j }=\frac { 2EI }{ L } (θ_{ i }+2θ_{ j }-3ψ)\\ ψ=\frac { v_{ j }-v_{ i } }{ L }$$

$$M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ L } ψ\\ M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ L } \left( \frac { v_{ j }-v_{ i } }{ L }  \right) \\ M_{ j }=\frac { 2EI }{ L } θ_{ i }+\frac { 4EI }{ L } θ_{ j }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }\\ M_{ j }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } { v }_{ j }+\frac { 4EI }{ L } θ_{ j }$$

$$V_{ i }=\frac { M_{ i }+M_{ j } }{ L } \\ M_{ i }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 4EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }\\ M_{ j }=\frac { 6EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ { L }^{ 2 } } v_{ j }+\frac { 4EI }{ L } θ_{ j }\\ M_{ i }+M_{ j }=\frac { 12EI }{ { L }^{ 2 } } { v }_{ i }+\frac { 6EI }{ L } θ_{ i }-\frac { 12EI }{ { L }^{ 2 } } v_{ j }+\frac { 6EI }{ L } θ_{ j }\\ \frac { M_{ i }+M_{ j } }{ L } =\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ { L }^{ 2 } } θ_{ i }-\frac { 12EI }{ { L }^{ 3 } } v_{ j }+\frac { 6EI }{ { L }^{ 2 } } θ_{ j }\\ { V }_{ i }=\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ { L }^{ 2 } } θ_{ i }-\frac { 12EI }{ { L }^{ 3 } } v_{ j }+\frac { 6EI }{ { L }^{ 2 } } θ_{ j }$$

$$V_{ j }=-V_{ i }\\ V_{ j }=-\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }-\frac { 6EI }{ { L }^{ 2 } } θ_{ i }+\frac { 12EI }{ { L }^{ 3 } } { v }_{ j }-\frac { 6EI }{ { L }^{ 2 } } θ_{ j }$$

NOTACIÓN MATRICIAL.

$$H_{ i }=\frac { EA }{ L } u_{ i }-\frac { EA }{ L } u_{ j }\\ V_{ i }=\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }+\frac { 6EI }{ L^{ 2 } } θ_{ i }-\frac { 12EI }{ L^{ 3 } } v_{ j }+\frac { 6EI }{ L^{ 2 } } θ_{ j }\\ M_{ i }=\frac { 6EI }{ L^{ 2 } } { v }_{ i }+\frac { 4EI }{ L } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 2EI }{ L } θ_{ j }\\ H_{ j }=-\frac { EA }{ L } u_{ i }+\frac { EA }{ L } u_{ j }\\ V_{ j }=-\frac { 12EI }{ { L }^{ 3 } } { v }_{ i }-\frac { 6EI }{ L^{ 2 } } θ_{ i }+\frac { 12EI }{ L^{ 3 } } v_{ j }-\frac { 6EI }{ L^{ 2 } } θ_{ j }\\ M_{ j }=\frac { 6EI }{ L^{ 2 } } { v }_{ i }+\frac { 2EI }{ L } θ_{ i }-\frac { 6EI }{ L^{ 2 } } v_{ j }+\frac { 4EI }{ L } θ_{ j }$$

Las relaciones fuerza desplazamiento pueden expresarse en notación matricial, así:

$$\begin{bmatrix} \frac { EA }{ L }  & 0 & 0 & -\frac { EA }{ L }  & 0 & 0 \\ 0 & \frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  & 0 & -\frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ L^{ 2 } }  & \frac { 4EI }{ L }  & 0 & -\frac { 6EI }{ L^{ 2 } }  & \frac { 2EI }{ L }  \\ -\frac { EA }{ L }  & 0 & 0 & \frac { EA }{ L }  & 0 & 0 \\ 0 & -\frac { 12EI }{ L^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  & 0 & \frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  \end{bmatrix}\begin{Bmatrix} { u }_{ i } \\ { \upsilon  }_{ i } \\ { \theta  }_{ i } \\ { u }_{ j } \\ { \upsilon  }_{ j } \\ { \theta  }_{ j } \end{Bmatrix}=\begin{Bmatrix} { H }_{ i } \\ { V }_{ i } \\ { M }_{ i } \\ { H }_{ j } \\ { V }_{ j } \\ { M }_{ j } \end{Bmatrix}$$

Donde:

$$K=\begin{bmatrix} \frac { EA }{ L }  & 0 & 0 & -\frac { EA }{ L }  & 0 & 0 \\ 0 & \frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  & 0 & -\frac { 12EI }{ L^{ 3 } }  & \frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ L^{ 2 } }  & \frac { 4EI }{ L }  & 0 & -\frac { 6EI }{ L^{ 2 } }  & \frac { 2EI }{ L }  \\ -\frac { EA }{ L }  & 0 & 0 & \frac { EA }{ L }  & 0 & 0 \\ 0 & -\frac { 12EI }{ L^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  & 0 & \frac { 12EI }{ { L }^{ 3 } }  & -\frac { 6EI }{ { L }^{ 2 } }  \\ 0 & \frac { 6EI }{ { L }^{ 2 } }  & \frac { 2EI }{ L }  & 0 & -\frac { 6EI }{ { L }^{ 2 } }  & \frac { 4EI }{ L }  \end{bmatrix}$$

«K» es la matriz de rigidez del elemento.

$$u=\begin{Bmatrix} { u }_{ i } \\ { \upsilon  }_{ i } \\ { \theta  }_{ i } \\ { u }_{ j } \\ { \upsilon  }_{ j } \\ { \theta  }_{ j } \end{Bmatrix}$$

«u» es el vector de desplazamiento (traslaciones y giros).

$$f=\begin{Bmatrix} { H }_{ i } \\ { V }_{ i } \\ { M }_{ i } \\ { H }_{ j } \\ { V }_{ j } \\ { M }_{ j } \end{Bmatrix}$$

«f» es el vector de fuerzas (y momentos).